前排提醒，我博客的 markdown 渲染器像坨 shit，还没法内联 latex，此类算法分析建议移步我的 Github Pages(建设中。。。)

做个DP题 (Beautiful Subsequence) 被卡时间qwq，不得不现学树状数组( Binary Indexed Tree )进行优化。

参考文章

实战

其实做完 Beautiful Subsequence 后对 BIT 怎么应用仍然处于一知半解的状态，但我觉得可以把一个 $O(n^2 \log n)$ 的遍历方法转换为 $O(n\log ^2 n)$ 属实是有点魅力的，于是我就仔细思考了一下这道题里树状数组到底是怎么应用的。

首先从一个很简单的应用开始，给定一个数组 a[22]，为了方便（其实是因为因为我做题时这样想的啦）我们从 1 开始下标

a[22] = {1 2 3 4 5 16 6 7 8 9 10 19 11 12 14 15 17 18 21 22 20 13}

对于每个 a[i]，我们想找出 a[1] ~ a[i-1] 中小于 a[i] 的数有多少个，显然可以直接暴力遍历，但需要花费 $O(n^2)$ 的时间，我们可以发现其实暴力遍历时有很多重复遍历，就举个最简单的例子，a[0]，这个数我们是在反复遍历的。那么这时候就可以用树状数组来储存我们遍历了的这些数的个数。

#include <iostream>
using namespace std;

int F[100001] = {0}; // sum(F[1:ind]) 储存目前已遍历数组内所有比 ind 小的数的个数

int lowbit(int x) {
    return x & (-x);
}

void add(int t[], int ind, int n, int k) {
    for (int i = ind; i <= n; i += lowbit(i)) {
        t[i] += k;
    }
}

int getSum(int t[], int ind, int n) {
    if (ind > n) return getSum(t, n, n);
    int sum = 0;
    for (int i = ind; i > 0; i -= lowbit(i)) {
        sum += t[i];
    }
    return sum;
}

int getSum_interval(int t[],int n, int L, int R) {
    if (L > R) return 0;
    return getSum(t, n, R) - getSum(t, n, L-1);
}

// (scanf 和 cout 混用的代码奇丑无比，别学我，会被开除的x)
int main() {
    int N;
    scanf("%d" , &N);
    int a[N + 1];
    for (int i = 1; i <= N; i++) {
        scanf("%d", &a[i]);
    }
    int ans = 0;
    for (int i = 1; i <= N; i++) {
        int num_leq_ai = getSum(F, a[i], 100000);
        int num_gt_ai = i - 1 - num_leq_ai;
        cout << "i = " << i << ": " << endl;
        cout << "the number less than or equal to a[i]: " << num_leq_ai << endl;
        cout << "the number greater than a[i]: " << num_gt_ai << endl << endl;
        add(F, a[i], 100000, 1);
    }
}

至于为什么可以这样做，关键在于理解我们每一次遍历完 a[i] 后做的 add(F, a[i], 100000, 1) 这个操作，我们做这个操作时，我们只遍历到了 a[i] 这个数，也就是说 a[i+1] 等 a[i] 后面的数此时对我们想要的结果是没有任何影响的。当我们遍历 a[i+1] 时，我们需要找到 a[0] ~ a[i] 中所有小于 a[i+1] 数对结果产生的累加影响，我们可以直接调用 sum[1:a[i+1]] 。至于为什么呢，还是那句话，关键要理解 add(F, a[i], 100000, 1) 在干什么，这个东西真的很难讲清楚，你去对着下面那张示例图多走几遍流程就明白了，我们每次做这个操作时，区间和 sum[1:a[i]-1] 是不受影响的，区间和 sum[a[i]:n] 是受影响的，此时我们再回忆下 sum[1:ind] 代表什么，代表 a[1] ~ a[i-1] 中小于 ind 的数的个数，我们会惊奇地发现这样操作竟然完美符合我们希望得到的结果，即当我们增加在原数组origin[a[i]](假设 BIT F[] 维护的原数组是 origin[]) 时，所有大于等于 a[i] 的 ind 我们都需要把结果加 1，而小于 a[i] 的 ind 我们不动它，符合预期。这样我们就把一个 $O(n^2)$ 的遍历降为了 $O(n\log n)$

其实更深一步理解，在遍历 a[i] 时，我们本质上是需要a[0] ~ a[i-1] 中所有小于 a[i] 的数对结果影响一个权值的加和，在统计个数时，这个权值等于 1 ，但我们能做的远不止加 1 这么简单，我们可以加任何权值，即 add(F, a[i], 100000, 1) 可以换成 add(F, a[i], 100000, k) ，其中 k 为我们需要的权值，这就是后面我们的 Beautiful Subsequence 所用到的技巧了。至于如果我们要求大于 a[i] 的数怎么办呢，我们可以求区间和sum[a[i]+1:n]。原理很简单，就是一个差集。

即可以把

int num_gt_ai = i - 1 - num_leq_ai;

换成

int num_gt_ai = getSum_interval(F, 100000, a[i] + 1, 100000);

应用场景：

1. 单点修改，单点查询
2. 区间修改，单点查询
3. 区间查询，区间修改

前置知识：

计算一个非负整数 n 在二进制下最低位位 1 及其后面为 0 构成的数。

例：44 = (101100)~2~，最低位 1 和后面的 0 构成的数为 (100)~2~ = 4

计算方法：

int lowbit(int x) {
    return x & (-x);
}

问题引入：

给出一个长度为 n 的数组，完成以下操作：

• 将第 x 个数加上 k
• 输出区间 [x, y] 内的每个数的和

显然，我们一开始会想到暴力的朴素做法，单点修改操作时间复杂度O(1)，区间求和，暴力遍历区间每一个数再相加时间复杂度O(n)，如果区间求和查询的次数为n次，那么中的时间复杂度为$O(n^2)$, 对于大数据的题来说肯定会 T，此时如果用树状数组的话复杂度可以讲到$O(n \log n)$.
树状数组的结构分析：

上面是树状数组的结构图，t[x]保存以x为根的子数中叶子节点值的和,原数组为a[]
那么原数组前4项的和t[4]=t[2]+t[3]+a[4]=t[1]+a[2]+t[3]+a[4]=a[1]+a[2]+a[3]+a[4],看似没有什么特点，别着急往下看

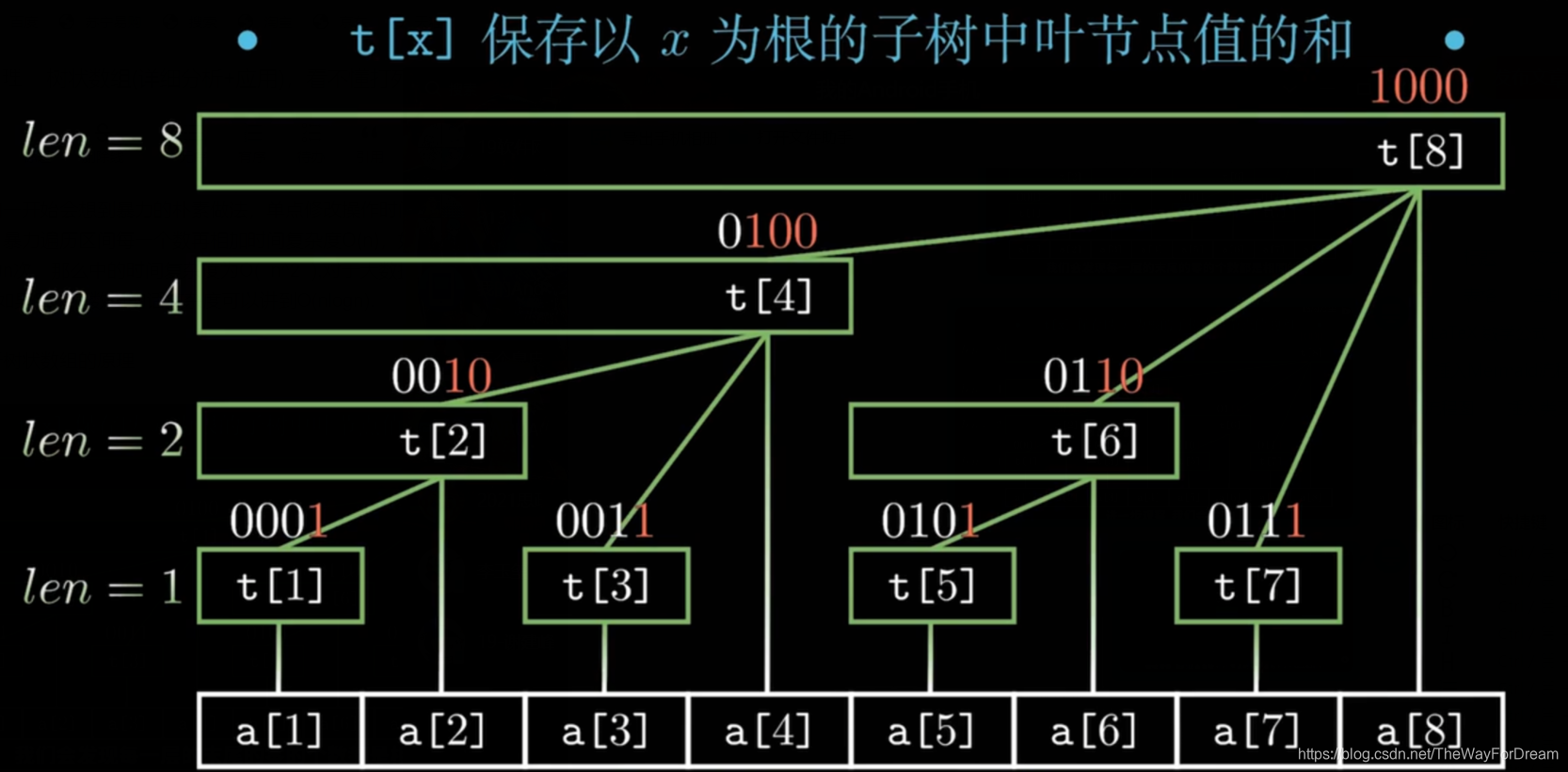
我们通过观察节点的二进制数，进一步发现，树状数组中节点x的父节点为x+lowbit(x),例如t[2]的父节点为t[4]=t[2+lowbit(2)]

树状数组的操作

单点修改和区间查询（二者绑定在一起，用树状数组维护原数组）

• 单点修改

  修改下标为 ind 的数，需要对其父节点进行依次更新，实现 a[ind] + k 代码如下：

  void add_single_point(int t[], int n, int ind, int k) {
    for (int i = ind; i <= n; i += lowbit(i)) {
        t[i] += k;
    }
  }

• 区间查询

  例，查询前 7 项的区间和 sum[7]（即求 sum[1:7]），从下图中可以看出，不断地减去 lowbit( i ) 直至 i 为 0 即可

  

  sum[i:j] 表示求原数组 a[] 下标为 i 到 j （包括 i 和 j ）的值。

  代码如下:

  int get_sum(int t[], int n, int ind) {
    // return sum[1:ind]
    // return 0 if ind is invalid
    if (ind > n) return get_sum(t, n, n);
    int sum = 0;
    for (int i = ind; i > 0; i -= lowbit(i)) {
        sum += t[i];
    }
    return sum;
  }

  如果要查询区间 [L, R] 的区间和，利用前缀和性质 sum[L:R] = sum[1:R] - sum[1:L-1]

  int search(int t[], int L, int R) {
    // return sum[L:R]
    // return search(t, R, L) if L > R
    if (L > R) {
        return search(t, R, L);
    }
    return get_sum(R) - get_sum(L - 1);
  }

区间修改和单点查询（二者绑定在一起，用树状数组维护差分数组）

• 区间修改

  对于这一类操作，我们需要构造出原数组的差分数组 diff_origin[] (diff[i]_origin = a[i] - a[i-1])，然后用树状数组去维护 diff_tree[] 即可。对于区间修改，只需要对查分数组进行操作即可，例如对区间 a[L, R] + k，在 diff_origin[] 中改变的只有 diff_origin[L] = a[L] + k - a[L-1] 和 diff_origin[R+1] = a[R+1] - (a[R] + k) ，于是在 diff_tree[] 中，我们只需要更新 add_single_point(diff_tree[], n, L, k) 以及 add_single_point(diff_tree[], n, R + 1, -k)

  代码如下：

  void add_interval(int diff_tree[], int n, int L, int R, int k) {
    add_single_point(diff_tree, n, L, k);
    add_single_point(diff_tree, n, R + 1, -k);
  }

• 单点查询

  由于我们维护的是原数组的差分数组，于是我们想单点查询时，需要明白 $\sum\limits_{i = 1}^{n}diff_origin[i] = a[i] - a[0] = a[i]$，于是就是求 diff_orgin[] 的前缀和，利用 diff_tree[] 可轻松求得。

  void ask_single_point(int diff_tree[], int ind) {
    return ask_sum(diff_tree, ind);
  }

区间修改，区间查询

这一类操作使用树状数组显得十分复杂，建议使用扩展性更强的线段树。