用高中生都能听懂的方式告诉你,音质真的不是玄学
我估摸着大部分人可能对音质都没什么要求,能“响”就行。但是对于一个靠音乐从地狱里爬出来的人,我希望听歌的每一分钟都是极致的享受,所以从最开始的只是想要换个好点的耳机消除电流声,到现在。。。虽然HiFi没有尽头,但当你的耳朵里回响着你最喜欢的音乐时,你会觉得这真的是人间最美好的享受,如同天籁一般,仿佛灵魂都要升华一般,啊,真爽啊~
追求听歌体验是件玄学,至少对于以前的我是这样的,为了不再漫无目的地追寻玄学,我一直在尝试更深入地理解什么叫做无损,什么叫做Hi-Res,至少要知道自己到底在追寻什么。那么现在,作为一个应该理解计算机最底层的人,我至少应该要知道我在听的歌在计算机里到底是怎么被记录的了。
现在,我也希望把我最近学到的一些东西用尽可能简单的方式分享给那些和我同样热爱音乐的朋友,去聆听音乐最本真的模样,表达我们对创作者的尊敬,也致敬我们热爱的音乐:cocktail:
先随便唠会嗑儿
我相信大家听歌时肯定都有选择过 标准品质、HQ高品质、SQ无损品质,现在某鹅厂音乐又加了一个臻品母带2.0 (虽然很过分的是居然又要再开超级会员:anger:)。那么不知道大家和我一样有没有好奇过这些品质到底有什么区别呢。诶我知道,听起来不一样,标准品质听起来糊糊的。那确实,可是有没有觉得品质提升到一定程度过后,声音不糊了,总感觉听出来的东西是一样的,听起来的感觉却不一样,没错,这就是玄学。别急,今天让我来陪大家聊聊这到底有多玄。
我先来从视觉的类比下直观地告诉你这是个什么玄学。
来看下下面这两段视频:
这是我用每秒10帧(每秒10张图片)制作的gif动图,
怎么样,看着还是知道这是个什么故事吧,
就是一个帅哥在用很炫酷的招式吊打另一个帅哥,打得都冒烟儿了~
但是看着还是很不舒服是吧,因为不够连贯,看久了还是有点晕。
接下来看一下原视频,原视频每秒是24帧(强烈建议看视频时拉下来点,把动图给遮住,体验好点,图床在github上,开了个转发代理,能访问,但有点慢,先往下读吧)
怎么样是不是舒服多了,看起来连贯多了,同一件事,不同的观感,听歌追求的音质也差不多这个意思,渴望拥有德芙般的丝滑。
以前我们平常看视频的帧率一般是30帧,现在条件好了就一般可以上到60帧,但是打游戏的同胞们知道,60帧也满足不了我们追求体验的需求了,要上高刷144帧。anyway,这是另外的故事了
对比到音乐中,我们平常听的歌一般就是44.1kHz采样率,16bit位深,2声道;在无损格式中一般会是48kHz,24bit位深,2声道;母带中一般会是192kHz,24bit位深,2声道。
听不懂?没事儿,别急,这篇文章就是告诉你这三个东西是什么的,这三个数字当然不是说无脑越大就越好,但总归是有点儿影响的,个人认为最影响的还是采样率了,至于为什么后面会提到。当然影响音质的不止这些东西,还有诸如压缩格式,播放设备,编解码等等,后面这些东西我也还没深究,等后续深究了再和大家分享~
音乐在电子设备里的学名叫数字音频,当然啦,数字音频不止包括数字音乐,还包括录音啦,演讲啦,总之只要是声音都能被记录下来,我不做这个方向(修正一下,可能今后要做音频方向了),音频处理的方向热度在计算机学术界可能比起视觉方面还是要稍欠火候,所以我们也不学音频相关的计算机知识,太深的东西俺也不敢乱讲,就只想从直觉的层面帮助大家理解下音质这个玄学的东西。
1. 什么是声音
首先,声音是怎么来的,相信初中物理课上老师拿个叉子震动乒乓球的画面在大家的脑海里还记忆犹深。这个实验说明了什么呢,我来帮大家回忆一下,这说明发声的物体是在震动的,只是震动太小,我们借助乒乓球这个辅助放大了这个震动让我们观察到震动这个现象。
后来我们学得更深入了,明白了声音的本质其实是波,像下面这样:
上面的视频中,我将一个正弦波的产生过程一点点地描绘了出来,我们的声音就是由一个个这样的正弦波的震动所产生的。我们都知道正弦波的函数是 $A\sin(w t + \phi)$ ,因此凭借函数我们可以知道任何一个时刻波的震动状态,但在现实中有两个因素导致我们无法知道声音在任意时刻的震动状态:
-
现实中的声音并不是简单的正弦波,而是由超级多频率不同、振幅不同、相位不同的正弦函数相加得来的复杂函数
-
在计算机的世界中,我们能模拟和操作的只有离散的值,针对连续的值的操作涉及对无限的操作,针对无限的直接操作是神的领域,至少我是这样认为的,anyway,关于无限高中生可能不是很能深刻理解,这是后话了。
什么是离散呢,如字面意思,就是分离的、分散的,就是一个个点的意思,往下继续看看也许你就能更理解什么叫离散了。这里我话痨的属性又上来了,有没有发现,我们针对所有事物的研究都想做到的是去把一个事物一步步地拆分开来,直到我们可以去研究去理解去操控,例如从声音>波,视频>一张张图片>一个个像素>一个个数字,从宏观物体>分子>原子>质子、中子、电子>夸克...
人类真的很聪明,总是会想办法去分解事物,直到事物可以被我们理解掌控,anyway,以后有机会再写些文章把我看到的一些科普性的东西和有趣的想法分享给大家,立个flag吧,至少把有关计算机最基础的知识给科普下。也许期末考完就写(maybe?)
坏了,既然我们无法知道一个波在任意时刻的震动状态那我们怎么描述这个波呢,别担心,办法总是有的,这时候离散的思想就帮上大忙了,这个办法是什么呢?
假设我们现在有了一堆曲线上的点 $(x,y)$ ,那么我们要怎么去描绘这个曲线呢?没错!就是你初中学的那一套,把点给画出来,然后用线给连起来。这就是我们在计算机中模拟音频信号的最基础思想:搜集足够多的点,用这些点猜出原来的波形是什么。那么接下来让我来为大家介绍模拟音频信号中的最核心的三个东西:采样率、位深、声道
2. 模拟音频信号
2.1 采样率
什么是采样率呢,还记得刚刚说过我们手上有一堆 $(x,y)$ 的点然后去描绘曲线吗?我们要怎么获得这一堆点呢?就是靠采样。下面的动画演示了采样的过程:
假设这段正弦波就是我们现实中的一个声音,显然在现实中这个波是连续的,但我们能记录的数是有限的,所以我们均匀地采集9个样点(红色的点)试图来表示这个波。我们将采样的点连起来是下面这样子的:
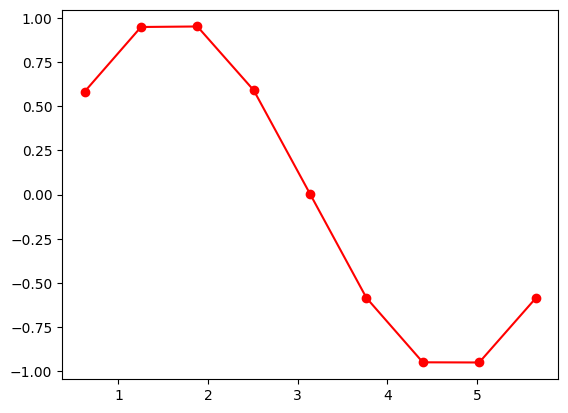
我们就借由这样的曲线来表示我们“听见”的这个正弦波。
当然实际中不只是这样简单的连线,会采用插值算法来填充采样过程中没采集到的点。
什么叫插值呢,简单来讲就是用相邻的两个点来猜中间那个点的值,比如我有两个点 (1,1), (3,3),然后我想要知道在 x=2 时对应的点,很自然的就会猜 (2,2),这就是最简单的插值算法。实际中采用的是惠特克—香农插值公式(Whittaker—Shannon interpolation formula),超出了我的理解范围(x)。
所以采样率代表什么呢?,没错,相信你已经猜到了,就是我们采样这些点的速度,1kHz就代表每秒钟采样1000个点。
采样率越高,声音重建的越完整,当然,这只是理论上的,实际上,根据奈奎斯特采样定理,我们只要以不低于于信号最高频率两倍的采样率进行采样就可以无损地还原出原来的信号,所以打电话时采样率一般为8kHz 因为人能发出的声音基本在4kHz以内。
我们人能听见的声音频率范围约为20 Hz – 20 kHz,所以一般音乐的采样率为 44.1kHz ,再高的采样率人耳也分辨不出来了,母带工程一般会采用192kHz的采样率,这样会保留音乐更完全的特征。既然高出来的采样率本质上人耳不能分辨,那不是蠢蠢浪费空间?你要从实用的角度那我确实无法反驳,但这是音乐,我们希望听到的肯定是音乐最最完整的声音,高出来的部分人耳或许不能分辨,但我相信人能感受,就像可见光之外的红外光和紫外光一样,人眼看不见,却总有办法感受它。(经过前端时间视唱练耳中的学习我也明白为什么了,因为现实中的声音是有泛音的,泛音可能会超出人耳听觉范围,但我们的身体是能对这些泛音有感受的)
位深
这个可以比较直觉地讲一下,普通的一般是16bit位深,上档次点的就是24bit位深,简单点讲就是我们能记录的 y 轴上的值,16bit理论上能记录的就 $2^{16}$ 个数,24bit理论上能记录 $2^{24}$ 个数,所以位深越大也是理论上记录的信息越多。理论上16bit位深就够用,母带的话会用 24bit。
我们都知道实数域中的数是无限的,因此我们只能记录有限的数,直观地表现就是下图中的这些纵坐标上的横线,每一条横线都是我们能记录的一个值,如果我们采样时点的数值在横线之外,那么很遗憾,我们只能舍弃部分精度用我们能记录的数字去表示它,所以这也是为什么位深越深,能还原的信息也就越多.

声道
声道数决定了音频的空间表现力。单声道(Mono)音频只有一个声道,所有声音都从一个单一的方向播放。立体声(Stereo)音频有两个声道,左和右,能够模拟宽广的空间感,让声音似乎从两边来。多声道音频(如5.1环绕声)使用更多的声道来创建更全面的空间音效。
大概意思就是左耳和右耳一边一个声道,不同的叠加方式可以营造出空间感,比如卜灵卜灵的声音围绕着你。
高解析度音频
最后想介绍一下Hires的音频。我相信你肯定看过这个小图标

这是什么意思呢,其实就是你的采样率高于普通的的44.1kHz或者位深比普通的16bit深就可以去申请这个小标标,这是索尼当初为了推广自家产品推出来的认证标准,说白了都是资本的营销手段,所以这个小金标现在到处都是,大家都可以见怪不怪。最能体现一个音频文件质量的就还是采样率和位深了,当然设备的质量也十分关键,比如收音设计,电容元器件这些也是十分有影响的,anyway,我们能看见的也就采样率和位深了,更多的不是科技工作者也不用考虑那么多了。



叨叨几句... NOTHING